


Curved spaces play an essential role in general relativity, where gravity is often visualized as curved space. Curved spaces can generally be described by Riemannian geometry though some simple cases can be described in other ways. It is still the question who was right? Newton, Maxwell, Bohr or Einstein? This article will discuss the interaction between “Gravity and Light” based on a deductive discussion based on the fundamental arguments and way of thinking within that corresponding time-frame.Curved space often refers to a spatial geometry which is not "flat", where a flat space has zero curvature, as described by Euclidean geometry. Maxwell who had built the “Mathematical Foundation for Electrodynamics”, Bohr (together with Heisenberg) who overruled Einstein during the 5th Solvay Conference in 1927 with the fundamental concept of “Quantum Mechanical Probability” or Einstein (his time-frame far ahead) who postulated a “Curved Space-Time Continuum” within a gravitational field.
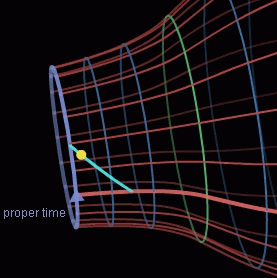
An interesting question would be: “Who would win the fundamental discussion about the interaction between “Gravity and Light” comparing the 4 fundamentally different time-frames? Newton, Maxwell, Bohr or Einstein? Newton with the fundamental “3rd law of equilibrium between the forces (force-densities)”.

Newton in the 16th century, Maxwell in the 18th century, Bohr in the 20th century and Einstein was physically living in the 20th century but he was his time far ahead and with his concept of a “curved space-time continuum” more connected to the 21st century. Isaac Newton, James Clerk Maxwell, Niels Bohr and Albert Einstein lived in fundamentally different time frames. From this paper we find that Clifford algebra has irreplaceable advantages in the study of geometry and physics. In the derivation of energy-momentum tensor, we obtain a spinor coefficient table Sabμν, which plays an important role in the interaction between spinor and gravity. In this paper, through a specific representation of tetrad, we derive the concrete energy-momentum tensor and its classical approximation. This uncertainty increases the difficulty of deriving rigorous expression. To study the interaction between space-time and fermion, we need an explicit form of the energy-momentum tensor of spinor fields however, the energy-momentum tensor is closely related to the tetrad, and the tetrad cannot be uniquely determined by the metric. Only in the new form of connection can we clearly define the classical concepts for the spinor field and then derive its complete classical dynamics, that is, Newton’s second law of particles. The representation of the new spinor connection is dependent only on the metric, but not on the Dirac matrix. To split the spinor connection into the Keller connection Υμ∈Λ1 and the pseudo-vector potential Ωμ∈Λ3 not only makes the calculation simpler, but also highlights their different physical meanings. By means of Clifford Algebra, a unified language and tool to describe the rules of nature, this paper systematically discusses the dynamics and properties of spinor fields in curved space-time, such as the decomposition of the spinor connection, the classical approximation of the Dirac equation, the energy-momentum tensor of spinors and so on.


 0 kommentar(er)
0 kommentar(er)
